By Charles L. Kane
Christopher H. Browne Distinguished Professor of Physics
University of Pennsylvania
Matter can arrange itself in the most ingenious ways. In addition to the solid, liquid and gas phases that are familiar in classical physics, electronic phases of matter with both useful and exotic properties are made possible by quantum mechanics. In the last century, the thorough understanding of the simplest quantum electronic phase—the electrical insulator—enabled the development of the semiconductor technology that is ubiquitous in today’s information age. In the present century, new “topological” electronic phases are being discovered that allow the seemingly impossible to occur: indivisible objects, like an electron or a quantum bit of information, can be split into two, allowing mysterious features of quantum mechanics to be harnessed for future technologies.
The building blocks of matter are largely known. Matter is composed of fundamental particles with electric charges that are precisely quantized in units of the indivisible fundamental charge e, and whose behavior is governed by the laws of quantum mechanics. In an atom, electrons with charge -e orbit the positively charged nucleus, similar to planets orbiting the sun. However, according to quantum mechanics, electrons can only exist in orbits with discretely quantized energy. This can make atoms electrically inert. Electrons are locked in place like legos: dislodging them requires a big enough kick to overcome the energy gap to the next discrete energy level.
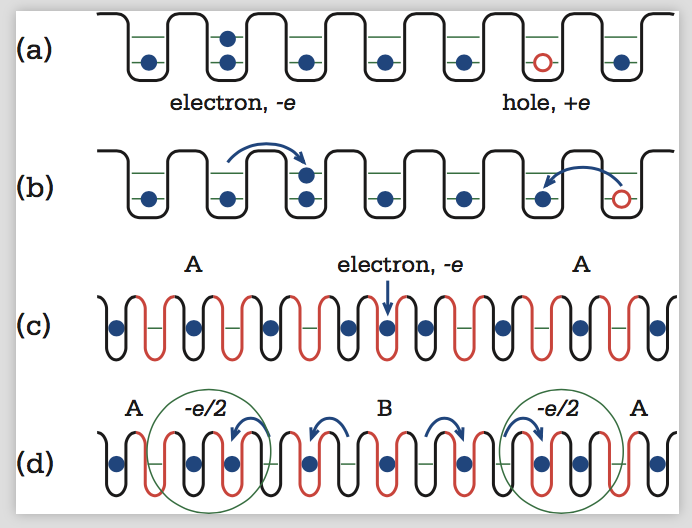
This simple picture allows a cartoon-like understanding of the insulating phase. In a crystal of inert atoms, all of the electrons are stuck on their home atom as in Fig 1a, allowing no flow of electric charge. There is a sense in which the insulating state is the most boring state: nothing happens. But if you add an electron to an insulator, that added electron can move around and conduct electricity. Alternatively, you can remove an electron. The missing electron, known as a “hole,” can also move when another electron takes its place, as in Fig 1b. Holes behave just like fundamental particles with charge +e, but they are not among the original building blocks. They are emergent particles that are fundamental excitations of the insulating state. They are also useful: most of modern electronics technology is founded on our exquisite control over electrons and holes. A semiconductor, like silicon, is an insulator to which electrons and holes can easily be added.
Of course, real materials are more complicated than the above cartoon picture. One of the triumphs of 20th century physics was the quantum theory of solids, which provides a detailed understanding of materials like silicon. However, there are things that the cartoon gets right. There is still an energy gap in silicon, and the fundamental excitations are still charge -e electrons and charge +e holes. The sense in which the cartoon “gets it right” leads to the deep and beautiful idea of topology. In your mind’s eye, you can imagine smoothly transforming a silicon crystal into a trivial atomic insulator by, for example, slowly moving the atoms apart. If along the way it remains an insulator with a finite energy gap, then there is a sense in which it has stayed the same. Topology is the mathematical study of objects that can be continuously deformed. The classic example for topology is the sense in which a doughnut is the same as a coffee cup. If they were made out of clay, you can imagine continuously molding one into the other. The thing that stays the same is the number of holes: the hole in the doughnut turns into the handle of the coffee cup. But not everything is the same. You can’t mold a ball into a doughnut without poking a hole in it—and you can’t do that smoothly. Insulators that can be continuously deformed into one another are topologically equivalent. Thinking about it this way poses a very interesting question that was overlooked for decades in the quantum theory of solids. Are there “topological insulators” that can not be smoothly deformed into trivial atomic insulators? The remarkable answer is yes, and they have fascinating, and potentially useful properties.
The simplest version of a topological insulating phase occurs in a one-dimensional (1D) polymer called polyacetylene, which is an electrical insulator that consists of a chain of atoms with alternating strong and weak bonds. However, there are two possible configurations (“strong-weak-strong-weak” and “weak-strong-weak-strong”) which are topologically different in the above sense. The cartoon picture for this insulator is that there are twice as many spaces for the electrons than there are electrons, so in the A-phase (B-phase) the electrons occupy only the black (red) sites in Fig. 1c. Importantly, there are just enough electrons to exactly compensate the positive charge of the nuclei, so that with half the spaces filled the system is overall electrically neutral.
Now, something magic happens when you add an extra electron, say, to the A-phase. In Fig. 1c there is one added electron, so the net charge is -e. In Fig. 1d, by simply shifting electrons over one space, that added charge -e splits in half! The only places where there is any net charge is in the regions where the electrons are bunched together. Since there are two of them they each have charge precisely -e/2. These -e/2 charges can move and are emergent particles in the same way that holes are.
How can this be? The electron is indivisible and can’t be split. But notice that between the -e/2 charges the insulator is in the B phase. The impossible” -e/2 charges exist on the boundary between topologically distinct insulators. This is the essence of topological phases of matter. They allow the indivisible to be split by putting the “impossible” on the boundary. There are many examples of this general phenomenon, and the impossible” things that they allow are truly remarkable.
Our first example is motivated by a problem: the flow of electrons in conductors is disorganized. It’s like trying to navigate a crowded hallway. You are constantly bumping into people, which makes it hard to get where you are going. This problem gets worse when the conductors are smaller, so this poses a serious obstacle to the miniaturization of electronics technology. How can we make the flow more organized? To organize traffic, we build divided highways. Can we do the same for electrons?
There exists a topological phase, called the quantum Hall state, that accomplishes this. This is the “mother of all topological phases:” the one we understood first and the one we understand the best. It was discovered in the 1980’s, when experimentalists making electrical measurements on semiconductor devices found a striking quantization of the Hall resistance when electrons were confined to a 2D plane in the presence of a strong magnet. This prompted theoretical physicists to think deeply about how that could be and to introduce the notions of topology that now underlie the field.
The quantum Hall state has an energy gap in the 2D interior, so the electrons are locked in place like in an insulator. However, it is topologically distinct from a trivial insulator. It necessarily has a “one-way” electrical conductor on its 1D boundary. These one-way edge states are remarkable because an electron in them has no choice but to go forward. This makes the electrical conduction perfect and leads to an electrical Hall resistance that is precisely quantized in units of the fundamental constant h/e² (h is Planck’s constant). Experimentally, this quantization is measured to one part in a billion. It is so accurate, that these measurements now serve to define the standard unit of resistance called the Ohm, which is a key part of the international system of units used by physicists.
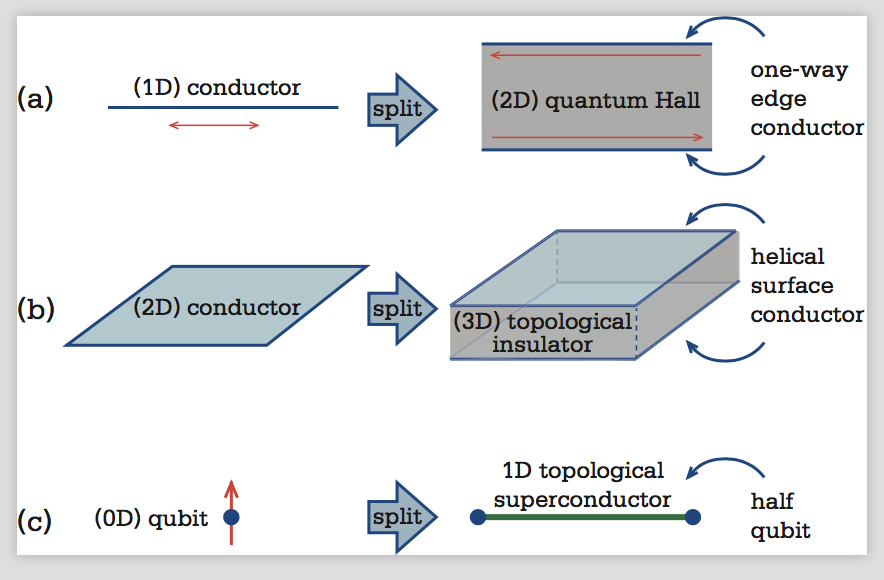
The one-way edge states are also remarkable because they are impossible. If they were to exist in isolation, deep principles of charge and energy conservation would be violated. An ordinary 1D conductor allows motion in both directions, with counterpropagating lanes that are inextricably tied to each other. The quantum Hall state allows those indivisible lanes to be split, as shown in Fig. 2a. Once you have a one-way edge state it is impossible to get rid of it. If you did, then the other edge would be an impossibly isolated one-way conductor. Thus, the edge states are topologically protected.
The one-way edge states could be useful for organizing the flow of charge in tiny electrical conductors. However, a difficulty is that using present technology a strong magnet is required to create them. There is another topological phase called a three-dimensional topological insulator (3D TI), which could provide a route towards that goal without the magnet.
A 3D TI is a material that is an insulator on its interior, but is a very special kind of electrical conductor (called “helical”) on its 2D surface. The helical surface conductor can be viewed as splitting an ordinary 2D conductor into two pieces: one on the top and one on the bottom (Fig. 2b). These helical conductors are impossible in isolation. They possess a special property called a “single Dirac cone” that is impossible in a purely 2D system. Once you have them, though, they are impossible to get rid of. Like the edge states in the quantum Hall effect they are topologically protected.
Unlike the quantum Hall effect, 3D topological insulators were conceived of by pure thought. Theorists realized that such a phenomenon was possible, and developed techniques to predict specific materials where it would occur. Experimentalists then created the materials and performed measurements that verified their properties. For example, a landmark experiment in 2008 observed the single Dirac cone on the surface of a crystal of Bi₂Se₃ using a technique called angle resolved photoemission spectroscopy. This helped initiate a vast subfield of condensed matter physics with strong interplay between theoretical physics, computational physics and experiment. Nowadays there are many more materials that are known to be 3D TI’s and related topological states.
One of the potential applications of topological insulators is to use them to organize the flow of electric charge in the tiny conductors. A second, more speculative but also more ambitious, proposal is to use topological insulators and related materials to construct a quantum computer. This problem motivates our third example of a topological phase.
Ordinary computers perform logic operations on bits: the 0’s and 1’s that can be combined to encode binary numbers. A quantum bit (or qubit), can be 0 or 1 or both at the same time. This combination of 0 and 1 is enabled by a mysterious feature of quantum mechanics called superposition. This allows a quantum computer—a device that performs operations on qubits—to be much more powerful than an ordinary computer. Unfortunately, a quantum computer is very hard to make because qubits are fragile. If you measure a qubit, you lose most of the information that it encodes. The difficulty is therefore making sure that the quantum computer doesn’t accidentally measure itself. This fact makes constructing a quantum computer one of the grand technological challenges for the coming century. One approach is to try to make the qubits very well isolated. There is another approach which takes advantage of a topological electronic phase.
The idea is to split the qubit. Qubits are ordinarily pointlike (0D) objects, like atoms or spins, that can exist in two distinct states. However, just as a
topological insulator can split an electrical conductor into two, there exists a related topological phase called a topological superconductor that can split a qubit into two pieces that reside at the two ends of a 1D material, as shown in Fig. 2c. The beauty of this is that the qubit is shared between the two ends and cannot be measured with any local measurement on one end. The quantum information is thus topologically protected, and immune from accidental measurement. One possible route to creating a topological superconductor is to combine an ordinary superconductor (which can easily be found) with a topological insulator, or a related topological material. There is promising experimental evidence that such topological superconductors can be created. Demonstrating that they have the capacity to store quantum information remains a challenge—but one which seems likely to be solved.
Knowing the fundamental building blocks of matter and the rules that govern them is only part of the story in physics. In 1687 Newton’s Principia laid out the fundamental rules of classical mechanics. It was much later that the concept of energy emerged as an organizing principle for understanding what matter that obeys Newton’s laws can do. Likewise, the rules of quantum mechanics were laid out in the early 20th century. Organizing principles, like topology, for understanding quantum matter are still emerging. This makes it an exciting time to be a physicist, because matter can arrange itself in the most ingenious ways! •

