Thursday April 24, 2014, Simons Center for Geometry and Physics Auditorium, Room 103
Reception at 5:00pm
Performance at 5:30pm Watch the Video
Featuring José Menor: Piano, Keyboard, Laptop
RMSonce: Laptop, Visuals
Performance Description:
José Menor & RMSonce Project is an audiovisual proposal that brings together two Spanish artists coming from different fields (classical music and experimental electronics), who share a passion for mathematics and related musical experimentation, which are the basis of this Project. José Menor (classical pianist and composer) and Francesc Martí, aka RMSonce (mathematician, electronic music composer and video artist) explore the interaction between the acoustic sound of the piano, electronic music and video art, using the mathematical approach as a starting point. Mathematical techniques determine both the musical and visual content of the performance. Each of the works is built on a base of mathematic equations, which generate sequences of pseudo-aleatoric numbers that serve as a ‘DNA’ of the piece. These successions of numbers are used freely to determine the parameters of all the piece’s elements: the piano score (sometimes creating sequences and patterns of extreme virtuosity), the electronic rhythms and sounds, the real‐time visual projections, as well as the overall structure of each piece, determining how each of the elements is related to the others, and therefore defining the overall musical form. Within this framework there are also spaces for improvisation, both musical—in the piano and the electronics—and visual. However, these spaces are always subordinated to the mathematic essence of each piece.
Concert Program:
Schrödinger (Passacaglia)
Iterations in F
Reflections
Uncertain ambient
Geometric Variations
Quantum cycles
MATH
As we have mentioned, the pieces are based on series of pseudo-random numbers, generated mostly with equations named linear congruential generators (LCG).
It is well known that linear congruential generators have been successfully used in recent years in musical composition applications. The special characteristics of such functions (periodicity, lattices, steady-state, etc.) cause that in many cases they can’t be considered as good random generators, and they can’t be used for applications where high-quality randomness is essential. But paradoxically, these problems may help to generate very interesting patterns that can be used in artistic creations.
These generators are based on the recursive formula
where x, a, c and m (the initial seed, the multiplier, the increment and the modulus) are integers and m>0, 0<a<m , 0<c<m and 0<x<m.
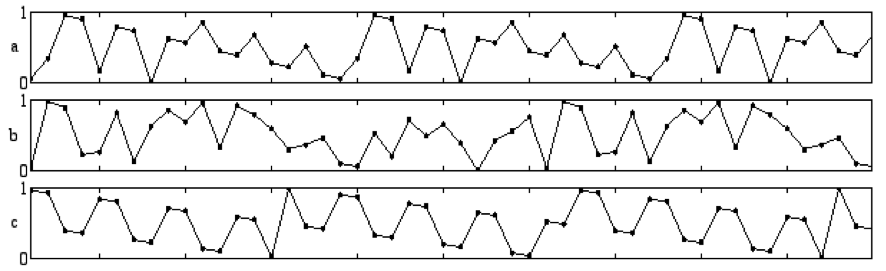
Therefore, each piece is based on a group of generators that are used to freely define all the elements of the piece. For example, graphically, three generators would create the successions a, b and c of the chart below, and these successions would be used to generate all the content of the pieces, including the piano score, the electronics and the visuals, as mentioned. For instance, the successions also allow us to control the granular synthesizer: when the grains of sound occur in time, they distribute them in space and determine the selection of their synthesis parameters: duration, amplitude, pitch, sample selection and sample position.
We also use a derivative of the LCG, the multiple recursive generator (MRG), which additively combines two or more generators. If n generators with periods m1, m2, . . ., mn are combined, then the resulting period is LCM (m1, m2, . . ., mn ), thus the period can be at most m1x, m2x, . . ., mnx.
Finally, in other works we also use the generator named Lagged Fibonacci Generator, a generator very similar to an LCG but it introduces a delayed feedback, using the transition function xn +1 = (xn xn – k ) mod m, where has been typically addition or multiplication.
ABOUT THE MUSICIANS
José Menor was hailed as ‘one of the most outstanding Spanish pianists of the new generation’ (The Daily Telegraph, Geoffrey Norris). José made his international debut at age fifteen, performing at New York’s Carnegie Hall as a First Prize winner of Cincinnati’s ‘The World Piano Competition’, which was followed by top prizes and awards at several different piano competitions (including YCAT in London or Viña del Mar in Chile). An experienced contemporary music performer, José maintains a close working relationship with renowned Spanish composers such as Héctor Parra or Joan Guinjoan, of whom he is the first pianist to have recorded his complete solo piano works (two-CDs), achieving outstanding reviews by the international press, including a four-star review at the prestigious Fono Forum magazine in Germany. José’s live performances have been recorded and broadcasted by different media including TVE (Spanish TV), TV3, CNN, RNE (Spanish National Radio), Catalunya Música, and has performed live on BBC Radio 3 (In Tune), Radio Canada, ABC Classic FM Australia, WXEL (USA), among others. José Menor was born in Sabadell (Barcelona), Spain, and studied piano, composition and conducting in Barcelona, followed by a Masters degree as a full-scholarship student at the Royal College of Music in London, and an Artist Diploma at the Yale University School of Music, studying with Peter Frankl and Claude Frank.
ABOUT THE MUSICIANS
RMSonce project is an experimental electronic music project founded in 2001 by the Barcelona-born mathematician, pianist, composer, programmer and video artist Francesc Martí. His three CDs (Opus e – 2002, The Game of Life – 2005 and Reflections – 2009), released by the Spanish label Medusa Music, have garnered many positives reviews from around the world. Francesc Martí has a bachelor’s degree in mathematics from the Autonomous University of Barcelona, a Master’s degree in Digital Arts from the Pompeu Fabra University and a Master’s degree in Free Software from the Open University of Catalonia. He also studied piano and composition at the Music Conservatory of Barcelona. Currently, He combines his art and technology projects with his teaching Audio Technology and Image at Open University of Catalonia, and a PhD in New Media Art at the De Montfort University of Leicester (UK).
For more information: http://www.josemenor.net/biografia_en.html