By Simon Donaldson
If we have four objects—say A, B, C, D—there are just three ways of dividing them into pairs:
(AB)(CD) (AC)(BD) (AD)(BC).
The salient property is that 3 is less than 4. This simple fact expresses something special about the number 4. For example if we take 6 objects there are 10 ways to divide them into triples; there are 35 ways to divide 8 objects into quadruples, 126 ways to divide 10 objects into quintuples and so on. We will discuss two famous applications of this special property of 4: one going back five centuries and one underlying important concepts in contemporary differential geometry and physics.

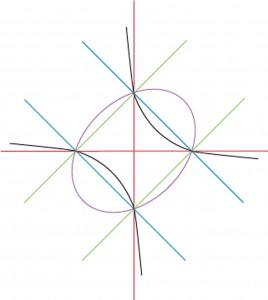
Intersection of conics. Image Simon Donaldson

Jim Simons speaks at the Dedication of the Iconic Wall, standing before Maxwell’s Equations. May 8, 2015. Photo Stony Brook University


