Organizing by:
- Benjamin Basso (Ecole Normale Superieure),
- Lance Dixon (SLAC/Stanford U.)
- Jaroslav Trnka (UC Davis)
- Anastasia Volovich (Brown)
This program will bring together physicists and mathematicians with expertise in different facets of particle scattering in planar N=4 super-Yang-Mills theory, in order to try to solve the theory for generic values of the coupling and kinematical variables.
It has been a long-standing quest to solve strongly-interacting four-dimensional relativistic quantum field theories by analytical methods. N = 4 super-Yang-Mills theory (SYM) is the “hydrogen atom” of gauge theories. It is the archetype for the AdS/CFT correspondence, connecting it to string theory and gravity, particularly at strong coupling. Perturbatively, its gluon scattering amplitudes closely resemble those for the gauge theory of the strong interactions, quantum chromodynamics (QCD). Hence it has proven indispensable as a testing ground for powerful new computational methods for precision collider physics. In the planar limit of a large number of colors (gauge group SU(Nc) with Nc → ∞), N = 4 SYM is integrable, and its scattering amplitudes are dual to the expectation values of Wilson loops for closed light-like polygons. The perturbative expansion of planar N = 4 SYM has remarkable geometric features, centered around polytopes related to various Grassmannians and the
differential forms that live on them.
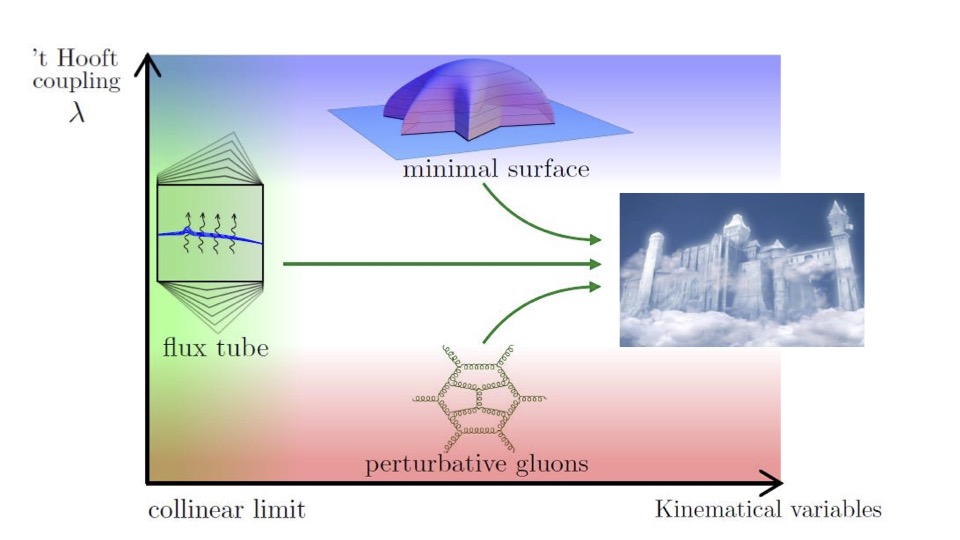
There are currently three independent descriptions of scattering amplitudes in planar N = 4 SYM, illustrated in the figure.
A weak-coupling formulation makes contact with perturbative methods involving Feynman diagrams; a “holographic” strong-coupling formulation employs minimal-area surfaces in Anti-de Sitter space; and a pentagon operator product expansion (POPE) approach exploits the two-dimensional integrability of a dual string picture at finite coupling in various kinematic limits. These formulations are all mutually consistent. (Indeed the compatibility of the POPE and perturbative approaches can be established through eight loop orders.) But they are formulated in mathematically very distinct ways, based on different underlying physical principles, and they make different properties of amplitudes manifest. In this program, the goal is to find a unified description of amplitudes in this theory that matches onto each of these formulations in the appropriate limit. Mathematically, the proposal is to search for functions that are able to interpolate between weak and strong coupling, for arbitrary kinematics, using all the knowledge we have about them in the respective limits. In this way one could gain a quantitative picture of how weak coupling excitations (gluons) evolve into strong coupling ones (strings) under a variety of physical circumstances. The spin-off for QCD could also be very important.
This program also has an associated workshop: Mathematical Aspects of N=4 Super-Yang-Mills Theory: February 26-March 1, 2024
MINI COURSE SCHEDULE
WEEK 1: January 8 – January 9, 2024
Monday 1/8/24: 1:30PM-2:30PM – Seminar Room – 313
Tuesday 1/9/24: 10:30AM-11:30AM- Seminar Room – 313
Tuesday 1/9/24: 1:30PM-2:30PM – Seminar Room – 313
Speaker: Lauren Williams
Title: The positive (tropical) Grassmannian, the amplituhedron, and cluster algebras
In this talk I will discuss the amplituhedron, focusing on the problem of finding tilings, as well as the connection to cluster algebras, such as the “cluster adjacency” phenomenon. I’ll start by describing what we know for the m=2 amplituhedron, including its connection to the positive tropical Grassmannian, and then I’ll describe the state of the art for m=4.
WEEK 1: January 10 – January 12, 2024
Wednesday 1/10/24: 10:30AM-11:30AM – Seminar Room – 313
Thursday 1/11/24: 10:30AM-11:30AM – Seminar Room – 313
Friday 1/12/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: Clément Dupont
Title: Motivic coaction for periods and amplitudes
The motivic coaction is a general structure of the algebra of periods (integrals on algebraic varieties) which extends the classical Galois theory of algebraic numbers. In these lectures I will give an introduction to this formalism and illustrate it with examples arising in particle physics. In particular, I will explain how the techniques of twisted cohomology explain the existence of a ‘cosmic Galois theory’ for Feynman integrals in dimensional regularization.
WEEK 2: January 16 – January 18, 2024
Tuesday 1/16/24: 10:30AM-11:30AM – Seminar Room – 313
Wednesday 1/17/24: 10:30AM-11:30AM – Seminar Room – 313
Thursday 1/18/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: Lionel Mason
Title: Strong Coupling and Minimal Surfaces
Alday & Maldacena conjectured an equivalence between string amplitudes in AdS5 ×S5 and null polygonal Wilson loops in planar N = 4 super-Yang-Mills (SYM). At strong coupling this identifies SYM amplitudes with (regularized) areas of minimal surfaces in AdS. In collaboration with Gaiotto, Sever & Vieira they introduced a Y-system and a thermodynamic Bethe ansatze (TBA) expressing the complete integrability that could in principle be used to solve for the amplitude. These lectures will review the parts of this material that we need and use them to identify new geometric structures on the spaces of kinematics for super Yang-Mills amplitudes. In AdS3, we find that the nontrivial part of these amplitudes at strong coupling, the remainder function, is the (pseudo-)Kahler scalar for a (pseudo-)hyper-Kaher geometry. It satisfies an integrable system and we give its Lax form. The result follows from a new perspective on Y-systems more generally as defining a natural twistor space associated to some integrable geometry. This connection to pseudo-hyperkahler and related geometries therefore extends to form-factors and full kinematics and suggests new structures underpinning the N=4 SYM amplitudes that might well be important beyond strong coupling.
Wednesday 1/17/24 – 1:30PM – Seminar Room 313
Speaker: Congkao Wen
Title: Exact integrated correlators in N=4 super-Yang-Mills theory
Over the past few years, it has been shown that, when integrating out the spacetime dependence with certain integration measures, some four-point correlation functions in N=4 super-Yang-Mills theory (N=4 SYM) can be computed exactly. These physical quantities are called integrated correlators. In perturbation, they are related to periods of certain conformal invariant Feynman integrals. Non-perturbatively, they are functions of (complexified) Yang-Mills coupling, and transform under the S-duality of N=4 SYM. In this talk, I will review some of the recent developments regarding these integrated correlators.
WEEK 3: January 22 -January 24, 2024
Monday 1/22/24: 10:30AM-11:30AM – Seminar Room 313
Tuesday 1/23/24: 10:30AM-11:30AM – Seminar Room – 313
Wednesday 1/24/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: Mark Spradlin
Title: Cluster Algebras and Symbol Alphabets
Abstract: Modern perturbative calculations of multi-loop amplitudes in planar N=4 SYM theory rely heavily on knowledge or assumptions about the types of functions that can appear and their singularity structure. I will review what is known, conjectured, and proposed about the connections between this structure and Grassmannian cluster algebras.
Thursday 1/25/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: Song He
Title: The unity of colored scalars, pions and gluons
Abstract: I will report on a new discovery that all-loop “stringy” amplitudes of tr phi^3 (the simplest theory of colored scalars) secretly contain the scattering amplitudes for pions and non-supersymmetric gluons in arbitrary dimensions. In particular, tree amplitudes of tr phi^3 , non-linear sigma model and Yang-Mills theory are given by expanding around different kinematic points of the same function, the Veneziano-Koba-Nielsen string amplitude, which in turn explains another surprise: tree amplitudes of all these colored theories have a hidden pattern of zeros and new factorizations near such zeros.
Friday 1/26/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: Carolina Figueiredo
Title: Gluons from Surfaces
Abstract: Scattering amplitudes for the simplest theory of colored scalars— Tr \phi^3 theory — have been understood as arising from a counting problem associated with curves on a surface (arXiv:2309.15913). This formulation produces “stringy” integrals for the amplitudes, built off of variables defined on the surface, from which the field theory limit as α′→ 0 can easily be extracted. Recently, extensions of this approach to theories closer to the real world — in particular the non-linear sigma model and Yang-Mills theory — have been proposed (arXiv:2401.05483,arXiv:2401.00041). In this talk, we will focus on the gluon case.
WEEK 4: January 29 – February 2, 2024
Tuesday 1/30/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: Aidan Herderschee
Title: Three Point Amplitudes in Matrix Theory
Abstract: The BFSS matrix model, a 1d matrix model that realizes 32 supercharges, is conjecturally dual to M-theory in eleven dimensional asymptotically flat space and provides a concrete example of celestial holography. Although the model could be viewed as a simpler version of N=4 SYM, it is in many ways more poorly understood. For example, there is no systematic proof that BFSS amplitudes obey the eleven dimensional Lorentz symmetry of the bulk theory. I will give a short overview of 2312.12592 where the three point amplitude in BFSS is computed by relating it to an index computation. I will first give a quick introduction to BFSS and motivate the computation. I will then outline how to compute the index in the matrix model and its relation to the 3-point amplitude. I will conclude with a short discussion of how one could use this result, in combination with other assumptions, to argue that generic BFSS n-point amplitudes are Lorentz symmetric in the large-N limit.
Wednesday 1/31/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: Henrik Johansson
Title: Constructing Non-Planar Integrands for N=4 SYM
Abstract: The many successes of the planar sector of N=4 SYM have not yet spilled over to the corresponding non-planar amplitudes, where the state-of-the-art calculations are at modest 4pt or 5pt level. While the planar integrand has been bypassed in favor of powerful amplitudes bootstrap methods, the integrand is still needed for non-planar N=4 SYM. The notion of a non-planar integrand is sometimes contentious, but for practical purposes a well-defined integrand can be obtained through standard unitarity-based calculations. I will discuss two new methods for bootstrapping the non-planar integrand of N=4 SYM, one of which was used to uniquely obtain a 6-loop 4pt integrand without any input from cuts constructed from complicated state sums. The two methods are universal, in the sense that they apply to any massless gauge theory.
Thursday 2/1/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: Andrew McLeod
Title: Bootstrapping Feynman Integrals via Landau Analysis
Abstract: Feynman integrals play a central role in perturbative quantum field theory calculations, and exhibit many intricate types of mathematical structure. In this talk, I will highlight recent progress that has been made towards untangling one important facet of this structure—the location and nature of their singularities. In particular, I will show how strong constraints can be placed on the analytic structure of Feynman integrals by connecting methods first pioneered by Landau to our modern understanding of the types of special functions that appear in perturbative computations. I will illustrate the power of these constraints by using them to bootstrap the complete functional form of several examples of Feynman integrals that involve both massive and massless particles.
Friday 2/2/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: Kai Yan
Title: Novel Aspects of Energy Correlators
Abstract: Energy Correlator observables probe the distributions of energy flow in the final states of particle scattering experiments.They provide valuable data for studies ranging from conformal field theories to jet substructure, and a potential playground for novel onshell methods in scattering amplitudes. We propose the study of N-point energy correlators in N=4 super Yang-Mills theory, as an integrated N+1-point super form factor of protected operators with manifest dual conformal symmetry. In the collinear limit, they admit parametric representations similar to Feynman loop integrals, linking to novel computational methods that operate directly in Feynman parametric space. We present the analytic result for the four-point energy correlator and comment on its singularity structures, which provide experiences for bootstrapping cross-section level observables.
WEEK 5: February 5 – February 9, 2024
Monday 2/5/24: 10:30AM-11:30AM – Seminar Room 313
Tuesday 2/6/24: 10:30AM-11:30AM – Seminar Room – 313
Wednesday 2/7/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: Amit Sever
Title: The OPE approach for scattering amplitudes
Abstract: One approach for computing planar scattering amplitudes in N=4 SYM theory is based on an analogue of an operator product expansion (OPE) for these observables. In this mini-course, we will review the main ideas of the amplitude OPE. We will start at weak coupling, bootstrap the finite-coupling OPE building blocks, and end with a reconstruction of the strong-coupling minimal area. A summary of extensions of the amplitude OPE and related open questions will be given.
Thursday 2/8/24: 10:30AM-11:30AM – Seminar Room 313
Speaker: Tianji Cai
Title: Transformers to transform Scattering Amplitudes Calculation
Abstract: AI for fundamental physics is now a burgeoning field, with numerous efforts pushing the boundaries of experimental and theoretical physics. In this talk, I will introduce a recent innovative application of Natural Language Processing to state-of-the-art calculations for scattering amplitudes. Specifically, we use Transformers to predict the symbols at high loop orders of the three-gluon form factors in planar N=4 Super Yang-Mills theory. Our first results have demonstrated great promises of Transformers for amplitude calculations, opening the door for an exciting new scientific paradigm where discoveries and human insights are inspired and aided by AI.
Friday 2/9/24: 10:30AM-11:30AM – Seminar Room 313
Speaker: Enrico Olivucci
Title: Multipoint Feynman Diagrams via Integrability
Abstract: Multi-point Feynman Diagrams (FD) in a d-dimensional CFT are highly nontrivial functions of conformal-invariants. To understand the class of functions that describes conformal FD is an intriguing open problem for the perturbative description of CFTs in d=4 dimensions, and data are usually hard to access beyond few loops. Following A. Zamolodchikov I will argue that here exists a wide class of conformal FD where the problem can be treated due to the braid “star-triangle” symmetry of the FD, allowing to formulate such integrals as partition functions of an Integrable spin-magnet in some infinite-dimensional representation of the conformal group SO(1,d+1). In particular, I will concentrate on the class of planar 4d Fishnet multi-point integrals with disk topology and derive an integrability-based representation over the spectrum of separated variables. In the simplest case of multi-point generalization of Davydichev-Usyukina Ladder integrals, I will explain how to get efficiently the light-cone-OPE in multiple channels, at any loop order.
WEEK 6: February 12 – February 16, 2024
Monday 2/12/24: 10:30AM-11:30AM – Seminar Room 313
Thursday 2/15/24: 1:30PM-2:30PM- Seminar Room – 313
Friday 2/16/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: Lance Dixon
Title: Amplitude Bootstrap
Abstract: Planar N=4 SYM amplitudes (and form factors) are dual to light-like polygonal Wilson loops (in a periodic space). They are nontrivial only for six or more gluons (three or more gluons). The spaces of functions which describe them are so restrictive that only a few constraints from the Pentagon OPE or other limits are needed to “write down the answer”, through seven loops in the six-gluon case, four loops in the seven-gluon case, and eight loops for the three-gluon form factor of the chiral part of the stress-energy tensor. I will review the construction of the relevant spaces of functions using the symbol and coaction. I will also describe a mysterious “antipodal self-duality”, which maps the four-gluon form factor into itself while reversing the order of all terms in its symbol, and which “explains” an antipodal duality between the three-gluon form factor and the six-gluon amplitude.
Friday 2/16/24: 1:30PM – 2:30PM – Seminar Room – 313
Speaker: Zhenjie Li (SLAC)
Title: Kinematics, cluster algebras and Feynman integrals
Abstract:Cluster algebras are found in not only amplitudes but also Feynman integrals in recent years. In this talk, I will provide evidence how cluster algebras appear in the alphabet of some planar kinematics of conformal Feynman integrals in four dimensions. They can be identified as non-trivial sub-algebras of the top-dimensional Grassmannian G(4,n) corresponding to n-point massless kinematics. By sending a point to infinity, this method applies for non-conformal planar Feynman integrals. With dimension reduction, it also provides some insight into the cluster algebra of Feynman integrals in 3D theory.
WEEK 7: February 19 – February 23, 2024
Tuesday 2/20/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: Chi Zhang
Title: Elliptic bootstrap program through Schubert analysis
Abstract: In this talk, I will briefly review the symbology for multiple polylogarithms and elliptic multiple polylogarithms with the sunrise integrals and the 10-point double-box integrals as examples. Then I will introduce the so-called Schubert problem and describe how to predict the symbol alphabet for the 12-point double-box integral using the Schubert problem and comment on the result obtained by the bootstrap program.
Wednesday 2/21/24: 10:30AM-11:30AM – Seminar Room – 313
Thursday 2/22/24: 10:30AM-11:30AM- Seminar Room – 313
Friday 2/23/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: James Drummond
Title: Solving N=4 Super Yang-Mills theory via Wilson Loops
Abstract: Scattering amplitudes are related to light-like (super) Wilson loops in N=4 Super Yang-Mills theory in the large N_c limit. I will recall some of the methods for computing such amplitudes/Wilson loops (e.g. BCFW recursion, Twistorial super Wilson loops and Qbar equations) and show that these methods extend to correlation functions of multiple Wilson loops.
WEEK 8: February 26 – March 1, 2024
Workshop: Mathematical Aspects of N=4 Super-Yang-Mills Theory
WEEK 9: March 4 – March 8, 2024
Monday 3/4/24: 10:30AM-11:30AM – Seminar Room 313
Tuesday 3/5/24: 10:30AM-11:30AM – Seminar Room – 313
Wednesday 3/6/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: Fernando Alday
Title: Tree level string amplitudes on AdS
Abstract: After reviewing properties of string theory amplitudes in flat space, in these lectures we will introduce a set of tools to construct tree-level string theory amplitudes on AdS Backgrounds, in a large radius expansion. This will combine the AdS/CFT duality, CFT tools, results from integrability and recent developments in number theory.
Thursday 3/7/24: 10:30AM-11:30AM – Seminar Room – 313
Speaker: Matthias Staudacher
Title: Brick wall diagrams as a completely integrable system
Abstract: We study the free energy of an integrable, planar, chiral and non-unitary four-dimensional Yukawa theory, the bi-fermion fishnet theory. The typical Feynman-diagrams of this model are of regular “brick-wall”-type, replacing the regular square lattices of standard fishnet theory. We adapt A. B. Zamolodchikov’s powerful classic computation of the thermodynamic free energy of fishnet graphs to the brick-wall case in a transparent fashion, and find the result in closed form. Finally, we briefly discuss two further candidate integrable models in three and six dimensions related to the brick wall model, and make some comments on the relation to the exact solution of integrable N=4 Super Yang-Mills Theory.
Thursday 3/7/24: 1:30PM-2:30PM – Seminar Room – 313
Speaker: Tomasz Lukowski
Title: Solving (strikethrough N=4 SYM) ABJM theory via scattering amplitudes
Abstract: In this talk I will introduce a remarkably simple positive geometry defined in the three-dimensional Minkowski space that encodes the integrands of scattering amplitudes for ABJM theory. For one-loop, the geometry is a curvy version of a simple polytope and its canonical differential form can be found for all multiplicities, providing previously unknown one-loop integrands for any number of particles. I will also comment on prospects for higher loops and other open questions.