By Kenji Fukaya
Recently there has been a discussion among mathematicians, as well as in press and several blogs, covering the developments in symplectic geometry. Professor Fukaya expressed interest in giving his opinion and we are happy to present it here:
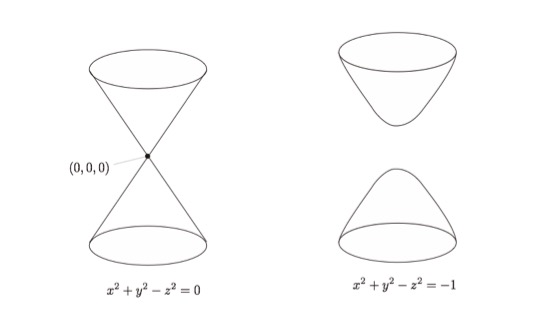
The set of the solutions of the equation x2 + y2 – z2 = 0 has ‘singularity’ at the point (x,y,z) = (0,0,0). On the other hand, x2 + y2 – z2 = -1 has no such singularity. (See the figure). Singular objects, such as x2 + y2 – z2 = 0 are very popular in algebraic geometry, the branch of mathematics that studies the space defined by
algebraic equations.
On the contrary, it is always difficult to include ‘singular spaces’ in differential geometry, or topology. A ‘manifold’ is the main target of research in those fields. The notion of a manifold goes back to Riemann, who introduced this concept as a space which looks like Euclidean space everywhere, locally. In other words, a ‘manifold’ is a space that has no singularity. It seems to me that there is still no reason to change this situation and shift the main focus of the field to the study of singular spaces. However, for the purpose of researching a manifold in differential geometry or topology, it also becomes important to study certain ‘singular spaces’ as a tool of the study.
In the 1970s, studying nonlinear differential equation on a manifold became an important part of differential geometry. In the 1980s it became important to research not only an individual solution of a nonlinear differential equation, but also the set of all solutions, as a whole. Such a set is called a ‘moduli space’. Using moduli spaces in differential geometry or topology was especially successful in two areas. One is the mathematical study of gauge theory and its application to the topology of low dimensional manifolds (such a study was initiated by S. Donaldson), and the other is the theory of pseudo-holomorphic curve in symplectic geometry (which was initiated by M. Gromov). Symplectic geometry is an area that started as a geometric study of the equations of classical mechanics.
Moduli space appeared in algebraic geometry much earlier than in differential geometry. When the foundation of modern algebraic geometry was built by the works of A. Weil, O. Zariski, A. Grotendieck, etc., the study of moduli spaces was one of the important reasons why extremely singular objects are included among the spaces to be researched.
In the differential geometric study of moduli spaces, people need to extract certain algebraic information from moduli spaces. The simplest information to be extracted is the number of points of such a space. Later on people started to extract more sophisticated information from spaces. Especially A. Floer, who found several versions of ‘Floer homology’, where he obtained groups rather than numbers from moduli spaces. With time, adding more structures to Floer homology became an important area of research and produced many applications.
To ‘count’ the number of points of a moduli space is actually a tricky problem. The number of solutions of the equation x2 = 0 is naively one since 0 is the only solution. However, it is more natural to regard it as two, since for any ϵ ¹ 0, the equation x2 = ϵ has exactly two solutions. In the world of algebraic geometry such a way to ‘count’ the number of points is known as ‘intersection theory’, and is closely related to the foundation of algebraic geometry. In the realm of differential geometry, singular objects are harder to study.
In the 1980s people used rather an ad-hoc method to find correct ‘count’ of the number of points of a moduli space.
When the study of moduli spaces in symplectic geometry made much progress it became necessary to find a more systematic way of such ‘count’. In 1996 several groups of mathematicians found it. We (K.F. and K. Ono) were one of them. Other groups included G. Tian, J. Li, G. Liu, Y. Ruan, and B. Siebert. This method is now called ‘virtual technique’.
By this method, two of the important problems of the field were solved. One is Arnold’s conjecture about the number of periodic solutions of Hamilton’s equation, an ordinary equation appearing in classical mechanics. The other is the construction of Gromov-Witten invariant, which is a basic invariant in the ‘topological version’ of string theory. When certain Floer homology is nonzero, it implies existence of a periodic solution of Hamilton’s equation. Gromov-Witten invariant is a ‘count’ of the number of solutions of a differential equation, non-linear Cauchy-Riemann equation.
These two problems had previously been solved under certain additional assumptions. By the new way to ‘count’ the number of points, it became possible to solve it in complete generality, in 1996.
When we found it, I believed this method would become a basic tool of the field. During the years 2000-2010, several important works used our version of virtual technique, which we called Kuranishi structure. J. Solomon’s and Melissa Liu’s important PhD theses both studied ‘open string analogue’ of Gromov-Witten invariant in two different situations and used Kuranishi structure. Ono used it to solve Flux conjecture, a famous open problem in symplectic geometry. Fan-Jarvis-Ruan built an important new theory, which they called ‘quantum singularity theory’. In the technical part of their theory, they used Kuranishi structure.
However, using Kuranishi structure did not become the standard of the field. Y. Eliashberg, H. Hofer, and S. Givental proposed a theory which they called Symplectic Field Theory. It uses the same kind of moduli spaces for its foundation. Hofer, together with K. Wyscocki and E. Zehnder, were building a version of virtual technique. They called it Polyfold. In those days, various people working in symplectic geometry mentioned on various occasions that Polyfold theory would soon be complete, becoming the standard by which all the previous approaches would be replaced.
I thought there could be many different approaches, each of which had its own advantage, to establish ‘the foundations of symplectic geometry’. On the other hand, for us (myself and my collaborators Y.-G. Oh, H. Ohta and Ono) the only way to persuade people to understand the importance of our approach was to continue working and to produce more applications.
As I mentioned, putting more structure to Floer homology was an important direction of our research. For this purpose, we needed to improve our method so that it could be safely used in more difficult situations. We were working on ‘Lagrangian Floer theory’, which is a version of Floer homology, and is related to ‘open string’ and ‘D-brane’. Our study was completed in 2009 and we wrote a two-volume research monograph. Soon after that, this theory was generalized by M. Akaho and D. Joyce. Joyce was not satisfied with our version of virtual technique and started a project to rewrite it. His way had various advantages compared to ours (and ours also had various advantages compared to his approach.)
We continued working on Lagrangian Floer theory. Our book in 2009 provided a foundation of the theory, but it did not contain much concrete calculations of the Floer homology we produced. For example, the notion called ‘bounding cochain’ is a major player of our theory. However, in 2009 the example of useful bounding cochain we knew was only 0. Later on, we found the first example of bounding cochain, which is far from 0 and is useful in the study of symplectic geometry. It was a solution of an equation x3 – x – Tα = 0 and is a complicated power series of T. Bounding cochain is a parameter to deform Floer homology. We found that, only at that particular value, Lagrangian Floer homology of a space (called CP2# – CP2 ) becomes nonzero. I was very happy when we found that an abstract notion ‘bounding cochain’, which is difficult to define and is hard to calculate, actually has highly nontrivial examples and is useful in symplectic geometry.
We thought that those generalizations and applications clarified the importance of our version of virtual technique in symplectic geometry.
Around that time, some people who had been ignoring our results, started asking us mathematical questions directly and suggested that there was a gap in our work. I was very happy to hear that, since serious mathematical communications with those people became possible at last, 16 years after we found it. A Google group called ‘Kuranishi’ was started in 2012, whose moderator was Hofer. There D. McDuff and K. Wehrheim posed several questions concerning the detail of our approach to virtual technique. We stopped our research on applications and concentrated on answering their questions in as much detail as possible. We replied to all of their questions. After 6 months no more questions were asked and the Google group was terminated.
I moved from Kyoto to the Simons Center for Geometry and Physics (SCGP) in that year. In
2013-2014, together with McDuff and J. Morgan, I organized a full-year program in SCGP on ‘foundations of symplectic geometry’. My motivation to organize this program was to provide people an occasion to present objections or questions to various approaches to virtual technique. We had two conferences, two lecture series, and many seminar talks. Many people visited SCGP during the conference, or other various periods of the program. During the program, Solomon presented an example which was related to certain issue in our approach. We wrote a paper to clarify this point,[1] which is recently published. Other than that we did not hear objections to our approach.
Hofer and Joyce gave a series of interesting talks presenting their approaches. There were other various approaches appearing around that time. Tian, together with B. Chen, wrote a paper to continue his way of studying virtual technique around 2005. Chen, together with B. Wang, also gave a talk on their approach at the SCGP during our program. One difference between their approach and ours is that we reduce problems to a finite dimensional geometry but they work directly in an infinite dimensional situation. D. Yang studied the relation between our approach and Polyfold theory. J. Pardon wrote a paper that put more emphasis on the algebraic side of the story. I think all of these different research methods contain various new and significant ideas.
The whole construction of ‘virtual technique’ consists of 3 steps. We start with nonlinear differential equation, Analysis. We then obtain some ‘singular space’ and study them, Geometry. Finally, we produce some algebraic structure, Algebra. If one works harder in one of those three parts, then in the other two parts the required amount of the work is smaller. In Polyfold approach, people work harder in analysis, and so less in geometry and algebra. In Pardon’s approach he works harder in algebra, and less in analysis and geometry. In ours and Joyce’s approach, we work harder in geometry, and so less in analysis and algebra. The difference between our approach and Joyce’s is that we study ‘singular space’ in a way closer to ‘manifold’, while Joyce studies it in a way closer to ‘scheme or stack’, the notion appearing in the foundation of algebraic geometry.
I think depending on mathematical taste and background, various researchers have different opinions on the version of virtual technique that is easier to understand and use. This is one reason why I think it is useful that various approaches will be worked out in detail — so that each researcher can choose their favorite one.
I think at this stage of 2017, it is becoming a consensus of the majority of the researchers of the field that, for the purpose to prove Arnold’s conjecture and Gromov-Witten invariant, all of those approaches will work. (The disagreement is mainly on when, where and who completed it. This is not related to mathematics and further discussion would be coarse and vulgar.
I am afraid to say, however, that for more advanced parts of the virtual technique such as those we have been developing since 2000-present, the consensus on its rigor, soundness, or cleanness is still missing. For example, McDuff and Wehrheim, in a paper arXiv:1508.01560v2 page 10, said that their version of ‘Kuranishi method’ is applicable only to Gromov-Witten invariant. Especially they denied its applicability to Floer homology. The purpose of much of my research since 2000 is to improve our version of virtual technique and widen the scope of its applications. Various people are now working on research in symplectic geometry and related areas such as Mirror symmetry, using various versions of virtual technique. I firmly believe that most of that research is based on sound, rigorous and clean foundations.[2] Unfortunately, this is not a consensus of the majority of the researchers of the field.
Together with my collaborators, I am trying to do my best to change this situation. I believe this effort contributes to the sound development of the field.
In this article I compared ‘the foundations of symplectic geometry’ to ‘the foundations of algebraic geometry’ several times. While I do think that symplectic geometry is as important as algebraic geometry, as regards to the foundations of the subjects at this time those of algebraic geometry have existed longer, and are broader. The foundations of symplectic geometry are parallel to the part of the foundations of algebraic geometry dealing with moduli spaces. One very important aspect of ‘the foundations of algebraic geometry’ is its application to number theory. There is nothing comparable to it in ‘the foundations of symplectic geometry.’
My dream is that in the future, virtual techniques will make some serious contribution to establishing the mathematical foundations of quantum field theory. If this dream comes true it could be comparable to the application of ‘the foundations of algebraic geometry’ to number theory. One could then say that ‘the foundations of symplectic geometry’ are comparable to ‘the foundations of algebraic geometry’. I believe there is a significant possibility that in the future this will actually happen.
[1] Shrinking good coordinate systems associated to Kuranishi structures, J. Sympl. Geom. 14 (2016).
[2] When we wrote the book on Lagrangian Floer theory in 2009, we made a few corrections to the definition of Kuranishi structure in our paper 1996. However none of its applications is affected by this correction. The definition we use now (2017) is equivalent to the one in our book of 2009.