The Iconic Wall is a site-specific permanent installation in the lobby of the Simons Center for Geometry and Physics, of stone carvings illustrating significant equations in math and physics.
The work is an impressive 279″ x 240″ x 2″ in size, filling a wall 465 square feet in area. In celebration of this significant work the Simons Center Gallery hosted an exhibition titled The Iconic Wall: Milestones in Math and Physics, co-curated by Lorraine Walsh, Art Director and Curator, Simons Center and Christian White.
The original concept of The Iconic Wall was proposed by Dr. Nina Douglas in 2010. The project was further developed by Dr. Douglas and Stony Brook Professor of Mathematics Anthony Phillips. Their design was then adapted by the artist Christian White for hand carving in limestone. The entire wall was carved in sixty-nine slabs of Indiana limestone by Mr. White and three other stone carvers. For the logistics of a permanent installation in the Simons Center, a rubber mold was made of each limestone slab and handmade lightweight casts of the individual slabs were created with cast stone. The carving and casting took a little over two years, and these casts formed the final installation in the Simons Center lobby.
The exhibition, Iconic Wall: Milestones in Math and Physics, featured a historical timeline detailing the equations and physical diagrams on The Iconic Wall. Also showcased were videos explaining the carvings and how the wall was made. Additionally, some of the original carved Indiana limestone was on view.
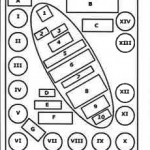
Key to Equations and Diagrams
I Jones polynomial for right trefoil knot; Witten’s path-integral formulation for Jones polynomial using Chern-Simons action.
II Associativity equation in QUantum Field Theory.
III Yang-Baxter equation.
IV Lorenz equations with orbit (Image: Scott Sutherland).
V Navier-Stokes equation with flow around cylinder (Image: J.D. Kim, AMS, Stony Brook)
VI The 5 regular polyhedra
VII Babylonian computation of √2. Tablet YBC 7289, Yale Babylonian Collection (Image: Bill Casselman).
VIII Visual proof of Pythagorean Theorem
IX Equiangular spiral drawn in “golden” rectangle (side ration = golden mean g); ratio of consecutive Fibonacci numbers approaches g, represented by its continued fraction expansion.
X Archimedes: volume of sphere. He had this figure carved on his tombstone.
XI Cell decomposition of torus; Euler characteristic; Gauss-Bonnet formula.
XII Diagram of black hole with Schwarzschild radius.
XIII Supergravity Lagrangian; root diagram of Lie group E8.
XIV Aharonov-Bohm effect
In Ellipse: (Kepler’s 1st law represented by star, ellipse, planet)
1 Kepler’s 2nd law.
2 Newton’s force-acceleration equation.
3 Kepler’s 3rd law
4 Newton’s gravitational law.
5 Einstein’s General Relativity equation
6 Schrödinger’s equation.
7 Dirac equation.
8 Atiyah-Singer Theorem.
9 Yang-Mills Equations.
10 Defining relation of Supersymmetry
In Background
A Einstein’s mass-energy equation
B Maxwell’s Equations
C Stokes’ Theorem
D The boundary of a boundary is zero.
E Heisenberg’s indeterminacy relation.
F Euler’s formula for Zeta-function
G Interaction between two strings; Feynman diagram shows corresponding interaction of particles, here the Compton scattering of a photon off an electron
